| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 해시테이블
- REST_API
- 프로그래머스
- Til
- 운영체제
- UX
- superstarjypnation
- redux
- vercel
- 백준
- Next.js
- html
- level1
- React
- 코드스테이츠
- 스택
- CSS
- web
- 큐
- 회고
- 생활코딩
- 프로토타입
- 카카오
- 자료구조
- 30daysdowoonchallenge
- javascript
- UI
- useState
- mysemester
- 자바스크립트
- Today
- Total
데굴데굴
힙 Heap 본문
공부자료: 신찬수 교수님 '자료구조' 재생목록
자료구조 힙 (heap) make_heap 연산 - YouTube
자료구조 힙 (heap) - insert와 delete_max 연산 - YouTube
*별도로 출처가 표기되지 않은 이미지는 직접 제작한 것
트리(tree): 부모-자식 관계를 계층적으로 표현한 자료구조
이진트리(binary tree): 부모 노드에 자식 노드가 최대 2개까지만 존재하는 자료구조, 두 개 이상의 노드가 올 수도 있지만 이진트리가 가장 많이 쓰임.
힙(heap): 특정 조건을 만족하는 이진트리

Tree Data Structures by C.Barkin Ozer | Medium
노드와 노드를 연결하는 선을 Edge 혹은 Link라고도 한다.
자식 노드가 없는 노드는 Leaf node라고 한다.
힙의 조건
1. 모양 성질
마지막 레벨을 제외한 모든 레벨의 노드는 채워져 있어야 함
마지막 레벨에서는 노드가 왼쪽부터 있어야 함.
2. 힙 성질
자식 노드는 부모 노드보다 값이 크면 안 됨.
즉, 힙 성질을 만족하는 모든 트리의 최댓값은 루트 노드이다.
표현법
1. 하나의 리스트에 표현
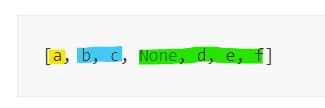
a = level 0
b, c = level 1
None, d, e, f = level 2
자식노드가 없을 떄에는 None으로 표기
규칙으로 노드를 찾을 수 있다.
루트는 무조건 a[0]에, 왼쪽 자식노드는 a[1]에, 오른쪽 자식노드는 a[2]에 저장됨.
노드 c (a[2])의 자식노드는 각각 a[5], a[6]에 저장됨.
--> a[k]에 저장된 노드의 왼쪽 자식노드는 a[2k + 1]에, 오른쪽 자식노드는 a[2k + 2]에 저장된다.
--> a[k]의 부모 노드는 a[(k-1)//2]에 저장됨.
장점: 규칙을 통해 자식 노드와 부모노드를 O(1)시간에 알 수 있다.
단점: 없는 노드도 표기하기 때문에 없는 노드가 많은 경우에는 메모리를 많이 차지함
2. 중복 리스트로 표현

3. 연결리스트로 표현
노드 하나에 부모 링크 하나, 자식 링크 두 개를 달아놓아 연결시킨다.
Heap 구현
1. Heap 클래스
class Heap:
def __init__(self, L=[]):
self.A = L
self.make_heap() # make_heap 함수 호출
def __str__(self):
return str(self.A)
def __len__(self):
return len(self.A)
2. heapify_down(k, n)
make_heap() 함수에 필요한 함수이다. 힙 성질을 만족하도록 리스트의 원소를 재배열하는 역할을 한다.
def heapify_down(self, k, n):
# k = 옮길 노드 번호, n = heap의 노드 수
# A[k]가 힙 성질을 만족하지 않으면 밑으로. 힙 성질을 만족하는 위치 찾기
while 2*k + 1 < n:
L, R = 2*k + 1, 2*k + 2
# m = 트리의 세 노드 중 최댓값을 갖는 인덱스, 부모/왼쪽/오른쪽 노드 중 최댓값 찾아 저장
if L < n and self.A[L] > self.A[k]:
m = L
else:
m = k
if R < n and self.A[R] > self.A[m]:
m = R
# k와 m 비교하기
if m != k:
self.A[k], self.A[m] = self.A[m], self.A[k]
k = m
else:
break
노드 k의 값이 노드 L, R보다 작다면 노드 k는 힙 성질을 위해 아래로 내려가야 한다.
k와 L, k와 R의 값을 각각 비교하여 세 노드 중 가장 큰 값의 인덱스를 변수 m에 저장해놓는다.
만약 k가 최댓값이 아니라면 (m과 다르다면) A[k]와 A[m]을 바꾸고, k가 최댓값이라면 종료한다.
3. make_heap()
def make_heap(self):
n = len(self.A)
for k in range(n-1, -1, -1):
self.heapify_down(k, n)맨 끝 노드부터 0번째 노드까지 heapify_down()을 수행하여 힙으로 만든다.
4. heap_sort()
def heap_sort(self):
n = len(self.A)
for k in range(len(self.A) - 1, -1, -1): # 맨 끝 노드부터 거꾸로 한 칸씩
self.A[k], self.A[0] = self.A[0], self.A[k]
n = n - 1
self.heapify_down(0, n)작은 값 - 큰 값 순으로 정렬해주는 함수이다.
5. find_max()
최댓값을 찾는 함수. 최댓값은 곧 루트노드이기에 루트노드를 출력한다.
값이 없을 경우도 고려한다.
def find_max(self):
if len(self.A) == 0:
return None
return self.A[0]
6. heapify_up()
def heapify_up(self, k):
while k > 0 and self.A[(k - 1)//2] < self.A[k]: # 부모 노드가 자식 노드보다 작을 때
self.A[(k - 1)//2], self.A[k] = self.A[k], self.A[(k - 1)//2]
k = (k - 1)//2heapify_down()과 반대로 밑에 있는 노드가 부모 노드보다 클 때 그 노드를 위로 올려주는 함수이다.
7. insert(key), delete_max()
def insert(self, key):
self.A.append(key) # 맨 끝에 값이 삽입됨
self.heapify_up(len(self.A) - 1) # 힙이 되도록 맨 끝 노드에서 업 수행
def delete_max(self):
if len(self.A) == 0:
return None
key = self.A[0] # 최댓값을 key에 저장해둠
self.A[0], self.A[len(self.A) - 1] = self.A[len(self.A) - 1], self.A[0] #swap
self.A.pop()
self.heapify_down(0, len(self.A)) #0번째 노드를 성질에 맞게 재배치
return key값을 새롭게 삽입하면 맨 끝 노드에 저장되므로 heapify_up을 호출해 힙 성질을 만족하도록 한다.
delete 함수에서는 최댓값을 key 변수에 저장해둔 후 맨 끝 노드와 루트 노드를 바꾸어 pop을 수행한다.
루트 노드로 올라간 값이 힙 성질을 만족하지 않으므로 heapify_down을 수행하여 힙으로 만든다.
저장해뒀던 최댓값인 key를 리턴한다.
파이썬에서 Heap 라이브러리 사용하기
파이썬에서 heap은 heapq라는 모듈로 내장되어 있다.
import heapq
h = []힙을 저장할 리스트를 만든 후 heapq.'연산 이름'('리스트 이름')의 형태로 연산을 수행한다.
제공 연산
1. heappush('리스트', key)
heapq.heappush(h, 3) # [3]힙 리스트에 원소를 추가한다.
2. heappop('리스트')
pop = heapq.heappop(h)
print(pop) # 3힙 리스트에 있는 최솟값을 지운 후 그 값을 리턴한다.
3. heapify('리스트')
A = [3, 2, 6, 12, 35, 32, 11, 17]
heapq.heapify(A)
print(A) # [2, 3, 6, 12, 35, 32, 11, 17]기존에 있는 리스트를 힙으로 변환한다.
heapq에서는 max heap이 아니라 최솟값이 루트 노드에 오는 min heap이 디폴트이다.
따라서 힙의 최솟값을 알고 싶다면 리스트의 0번째 인덱스를 호출하면 된다.
'CS > 자료구조' 카테고리의 다른 글
| 균형이진탐색트리 Balanced Binary Search Tree / 회전 Rotation (0) | 2022.07.26 |
|---|---|
| 이진트리 Binary Tree , 이진탐색트리 Binary Search Tree (0) | 2022.07.25 |
| 해시테이블 Hash Table과 Chaining (0) | 2022.07.09 |
| 해시테이블 Hash Table과 Open Addressing (0) | 2022.07.09 |
| 양방향 연결리스트 Doubly Linked List (0) | 2022.07.04 |


